Guia para Planejamento e Execução de Teste A/B

O Teste A/B é uma abordagem poderosa para medir o impacto de mudanças em produtos, interfaces ou estratégias, garantindo decisões fundamentadas em dados. Este artigo explora como planejar, executar e interpretar experimentos A/B, desde os fundamentos teóricos até a implementação prática.

---

1. O Que é um Teste A/B?

Testes A/B aplicam estatística inferencial para comparar duas ou mais versões de uma variável, avaliando qual delas gera melhores resultados. É amplamente utilizado em áreas como marketing digital, design de interfaces e otimização de produtos.

Motivação

Imagine que você deseja lançar um novo design de página web. A pergunta é: O novo design realmente aumenta a conversão?
Os Testes A/B ajudam a responder essa questão de forma objetiva.

---

2. Estruturando o Experimento

Um experimento bem planejado é essencial para garantir resultados confiáveis.

2.1 Escolha do Método

A base do experimento está no teste de hipóteses estatísticas, que avalia se os dados suportam uma hipótese particular.

• Hipótese Nula (H₀): Supõe que não há diferença entre os grupos.
• Hipótese Alternativa (H₁): Sugere que há uma diferença significativa.

2.2 Tipo de Teste

• Unicaudal (One-Tailed): Avalia mudanças em uma única direção.
  Exemplo: O novo design aumenta a conversão?

• Bicaudal (Two-Tailed): Avalia mudanças em qualquer direção.
  Exemplo: O novo design altera a conversão?

---

2.3 Definição das Variáveis

1. Variável Dependente: Métrica de avaliação (ex.: taxa de conversão).
2. Variável Independente: A mudança sendo testada (ex.: design da página).

---

3. Planejamento do Teste

3.1 Separação dos Grupos

• Grupo Controle: Representa o cenário atual.
• Grupo Tratamento: Recebe a alteração proposta.

3.2 Determinando o Tamanho da Amostra

Amostras muito pequenas podem levar a resultados inconclusivos, enquanto amostras excessivas podem ser caras e demoradas.

Fatores a considerar:

1. Effect Size: A diferença mínima relevante entre os grupos.
2. Nível de Significância (α): Probabilidade de rejeitar H₀ quando é verdadeira (erro tipo I). Geralmente, α = 0.05.
3. Poder Estatístico: Probabilidade de detectar uma diferença real (1 – β, sendo β o erro tipo II).

Por quanto tempo coletar dados do teste? O resultado do teste de hipotese (p-valor) vai depender da real diferença entre os tratamentos A e B, e também da sorte na amostragem.

Quanto maior a real diferença entre os tratamentos, maior a probabilidade do experimento revelá-la, e quanto menor a diferença mais dados serão necessários.

Assim, Poder ou Potência (Power) é a probabilidade de detectar um tamanho de efeito específico com uma amostragem com características específicas (tamanho e variabilidade).

import statsmodel.api as sm

effect_size = sm.stats.proportion_effectsize(0.0121, 0.011) #melhora de 10% = de 1,1% para 1,21%
analysis = sm.stats.TTestIndPower()
result = analysis.power(effect_size, # O tamanho do efeito calculado anteriormente
                        nobs1, # Número de observações no primeiro grupo (grupo de controle)
                        alpha, # Nível de significância (probabilidade de cometer um Erro Tipo I, por exemplo, 0.05
                        ratio=1.0, # A proporção entre os tamanhos dos dois grupos (tratamento e controle). O padrão é 1.0 (grupos do mesmo tamanho)
                        alternative='larger' # 'two-sided' para teste bicaudal ou 'larger' para teste unicaudal
)
print('Power: %.3f' % result)

O procedimento consiste em realizar re-amostragem dos dados de cada grupo, definir se o efeito é significativo para cada repetição, e por fim calcular a probabilidade em que resultados com significância foram encontrados.

Fórmula para Tamanho da Amostra

Note que já definimos o poder estatístico para 80%, é frequentemente considerado adequado em estudos estatísticos.

from statsmodels.stats import api as sm

sample_n = sm.NormalIndPower().solve_power(
    effect_size=effect_size,
    power=0.8,  # Poder estatístico de 80%
    alpha=0.05  # Nível de significância
)
print(f"Tamanho mínimo da amostra: {sample_n}")

---

3.3 Análise de Custo-Benefício

Antes de executar, avalie se o teste é financeiramente viável. Por exemplo:

• Queremos alterar a página de checkout do nosso produto.
• O custo de desenvolvimento da mudança é R$ 75 mil.
• O faturamento no ano é de R$ 2.190 mil.
• Para “pagar” o custo, o aumento de conversão esperado deve gerar um retorno de R$ 75 mil em um ano.
• Se o novo design aumenta as vendas em 3,42% (75k/2190k), o teste justifica a implementação.

Além do retorno mínimo, também é necessário analisar a viabilidade da coleta da amostra mínima necessária. A quantidade de dados necessária talvez demore muito tempo para ser coletada e seu custo (queda na conversão) acaba inviabilizando o teste.

---

4. Execução do Teste

4.1 Coleta dos Dados

• Estrutura: Crie um sistema robusto para coletar dados.
• Identificação: Use flags para separar grupos controle e tratamento.
• Ferramentas: Plataformas como Google Optimize, Optimizely ou scripts customizados.

4.2 Preparação dos Dados

• Limpe dados faltantes ou inconsistentes.
• Certifique-se de que as amostras sejam aleatórias e representativas.

4.3 Validação Temporal

Para casos em que os dados seriam coletados em menos de 7 dias, é definido como uma regra geral que a coleta de dados deve durar no mínimo uma semana, para abranger um ciclo sazonal (coletar dados com a variação natural de existente em cada dia da semana).

---

5. Testando as Hipóteses

5.1 Escolha do Teste Estatístico

A escolha do método depende da natureza dos dados:

1. t-Test: Para comparar médias de dois grupos.
2. ANOVA: Para comparar mais de dois grupos.
3. Chi-Squared: Para proporções categóricas. No nosso blog, você encontra um artigo completo sobre o teste qui-quadrado com exemplos práticos e aplicações em Python, ideal para aprofundar seu entendimento e aplicar em seus projetos.

Código em Python

from scipy.stats import ttest_ind

t_stat, p_value = ttest_ind(grupo_controle, grupo_tratamento)
print(f"p-valor: {p_value}")

---

5.2 Interpretação do p-Valor

• Se p < α: Rejeitamos H₀, indicando diferença significativa.
• Se p >= α: Não há evidência suficiente para rejeitar H₀.

Pensando no exemplo anterior, assumindo a hipótese que a variação da página B não causou nenhum aumento significativo na conversão, eu tenho certeza absoluta que não existe diferença entre as conversões das páginas.

Assim, espero que os valores de conversão não sejam muito diferentes, mas observar um valor muito distante, pode ser que ele seja causado pela aleatoriedade do experimento, já que eu tenho certeza de que não existe uma diferença.

Se a probabilidade desse valor distante acontecer for grande, significa que o efeito da aleatoriedade é tão grande que eu não posso ter certeza que o efeito observado foi causado pela página.

---

6. Conclusões e Ações

6.1 Validação dos Resultados

1. Reavalie as hipóteses iniciais.
2. Analise o impacto prático da mudança (ex.: aumento de conversão, receita adicional).

6.2 ROI do Teste

Calcule se o aumento justifica os custos.
Exemplo: Um aumento de 3,5% na taxa de conversão gerou R$ 80 mil de lucro adicional em um ano, superando os custos.

---

7. Boas Práticas

1. Nunca Teste Toda a Base: Use uma amostra menor para minimizar riscos. Se a página tem 1 milhão de visitantes nunca divida 500 mil para cada teste, mas sim uma fração menor, 10 mil para realizar o teste.
2. Análise Multidisciplinar: Alinhe-se com engenheiros, analistas e stakeholders.
3. Validação Repetida: Execute múltiplos testes para confirmar os resultados. Mas lembre de aplicar correções para controlar o erro do Tipo I (falsos positivos).
4. Documentação: Registre todas as etapas e resultados para aprendizado futuro.

---

8. Exemplos Avançados

8.1 Medindo o Effect Size

Cohen’s d: Avalia a magnitude do efeito entre dois grupos.

from pingouin import compute_effsize

d = compute_effsize(grupo_controle, grupo_tratamento, eftype="cohen")
print(f"Tamanho do efeito: {d}")

Glass’ Delta: Usa apenas o desvio padrão do grupo controle.

d = compute_effsize(grupo_controle, grupo_tratamento, eftype="glass")
print(f"Tamanho do efeito: {d}")

Hedge’s g: Corrige viés para amostras pequenas.

d = compute_effsize(grupo_controle, grupo_tratamento, eftype="hedges")
print(f"Tamanho do efeito: {d}")

---

9. Dicas para Decisões Estratégicas

• Trade-Offs: Para efeitos menores, maior amostra será necessária.
• Impacto Prático: Pequenas mudanças podem ter grande impacto financeiro.
• Iteração Contínua: Teste, aprenda e aplique melhorias constantemente.

---

Existem diversos testes de hipóteses, cada um pensando para um caso específico. Abaixo deixo um fluxograma para determinação de qual teste deve ser utilizado.

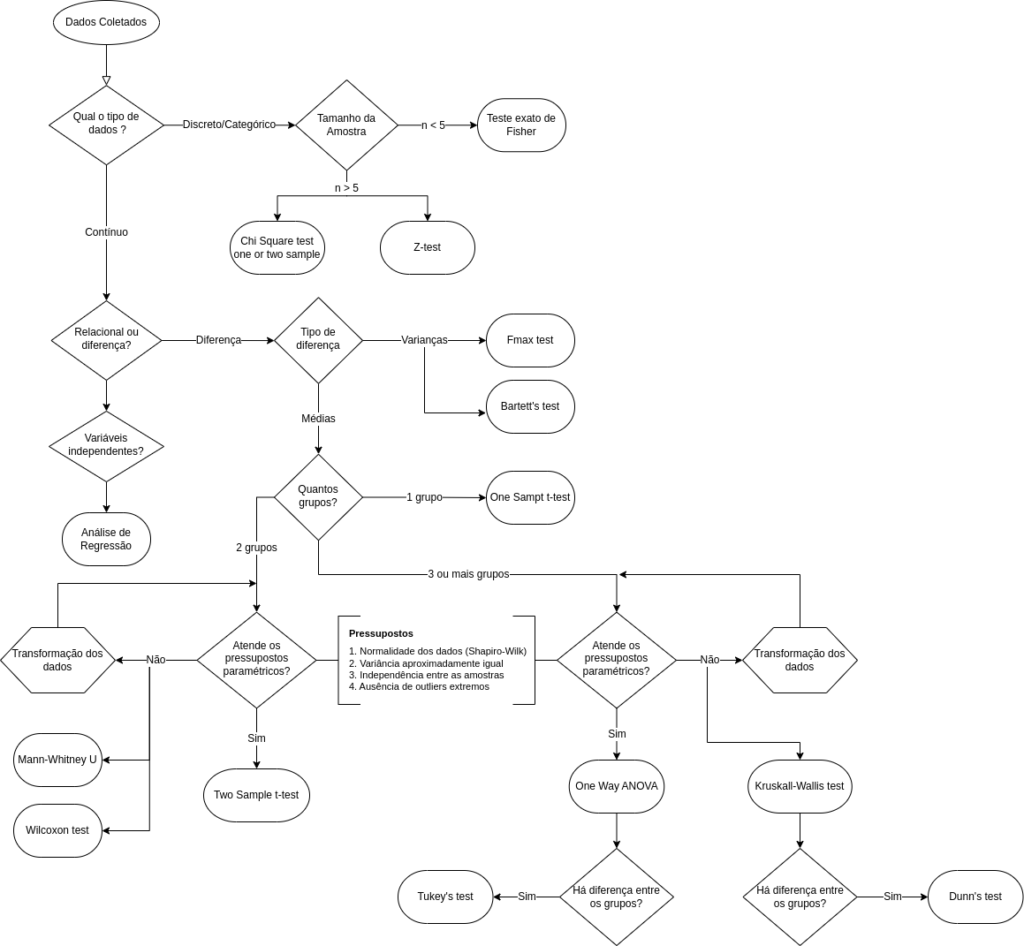
Conclusão

Testes A/B são fundamentais para a tomada de decisões baseada em dados. Ao seguir este guia, você pode maximizar a confiabilidade de seus experimentos e garantir que cada decisão seja respaldada por evidências sólidas.

Gostou do artigo? Compartilhe suas dúvidas ou experiências nos comentários! 🚀

Imagem de capa por Ab Testing Vectors via Vecteezy.